.rst .pdf

repository open issue suggest edit

Contents

Math basics

In this document we want to explore the most fundamental mathematical concepts which are needed for the basics of machine learning. This guide can not even scratch the surface of the tremendous amount of topics which should be covered but we can try nonetheless.

We will also discuss the notion that is used throughout the course.

A recommended read for a quick introduction is [Bur19].

Data structures

Scalar

We define a scalar \(x\) as a single numerical value and we note it as a single lowercase letter. Examples for a scalar can be a whole number like \(2\) or a real number like \(0.25\).

Vector

A vector \(\text{x}\) is a list of \(n\) scalar values with a fixed ordering of this collection. We call this an n-dimensional vector. For example \(\text{a} = [3, 2]\) is a 2-dimensional vector. We denote the \(i\)-th value of a vector \(\text{x}\) via \(x^{(i)}\), so in our example \(a^{(1)} = 3\). This index also denotes the dimension of a vector.

Matrix

A \(n \times m\) matrix \(\text{A}\) is an collection of numerical values which consists of \(n\) rows and \(m\) columns. The values of such are matrix are arranged as

\[\begin{split}\text{A} = \begin{pmatrix} a_{1,1} & \cdots & a_{1,m} \\ \vdots & \ddots & \vdots \\ a_{n,1} & \cdots & a_{n,m} \end{pmatrix}\end{split}\]

Set

A set \(\mathcal{S}\) is a collection of unique elements, so e.g. \(\mathcal{A} = \lbrace 5, 4 , 20 \rbrace\) or \(\mathcal{B} = \lbrace x_1, x_2, \dots, x_{n} \rbrace\). Common sets are the set of all real numbers \(\mathbb{R}\) or the set of all natural numbers \(\mathbb{N}\). We call a set of vectors a vector set.

We denote \(b\) is an element of a set \(\mathcal{B}\) by writing \(b \in \mathcal{B}\) or in the opposite when an element \(c\) is not contained in the set \(\mathcal{B}\) by writing \(c \notin \mathcal{B}\).

We denote the cardinality of a set \(\mathcal{S}\) as \(|\mathcal{S}|\) defined as the number of elements in the set \(\mathcal{S}\), so with our examples from above we have \(|\mathcal{A}| = 3\) and \(|\mathcal{B}| = n\).

The cardinality of a set can either be finite (such as \(\mathcal{A}\) and \(\mathcal{B}\)) but they can also contain an infinite amount of elements such as \(\mathbb{R}\).

Suppose we have two elements \(a\) and \(b\). If a set includes everything between \(a\) and \(b\) and also \(a\) and \(b\) itself we define it as a closed interval which is denoted as \([a,b]\). If \(a\) and \(b\) are not included in this set we define it as an open interval denoted as \((a,b)\).

Functions

A function \(f: \mathcal{X} \rightarrow \mathcal{Y}\) transfers each element \(x \in \mathcal{X}\) to a single element \(y \in \mathcal{Y}\) where \(\mathcal{X}\) is defined as the domain of a function and \(\mathcal{Y}\) as the co-domain. We often use the notation \(y = f(x)\). An example for this would be \(f: \mathbb{Z} \rightarrow \mathbb{N}\) which is defined by \(f(x) := x+4\) where \(\mathbb{Z}\) is the set of all rational numbers and we use \(:=\) to say that something is defined by the equation.

Of course domain and co-domain can be the same such as in \(g: \mathbb{R} \rightarrow \mathbb{R}\) which is defined by \(g(x):= x^2\). We see that the notion of the domain and co-domain is quite important and also allows us to shift between dimensions, e.g. the euclidian metric \(d(p,q) = ||p-q||_{2}\) of two vectors \(p, q \in \mathbb{R}^n\) is defined as

\[d(p,q) = ||p-q||_{2} := \sqrt{(q_1 - p_1)^2 + \dots + (q_n - p_n)^2 } = \sqrt{\sum_{i=1}^{n} (q_i - p_i)^2 }\]

so \(d: \mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}_{\geq 0}\). Although we provide high dimensions as input for our function we will receive a single scalar value as output of the equation. The euclidian metric is an instance of a metric which defines a distance between two points in a vector space and therefore has to meet certain criteria. A metric will be a crucial guideline for us when we are working in high, non-imaginable dimensions.

Minimum maximum

We define the local minimum of a function \(f: \mathcal{X} \rightarrow \mathcal{Y}\) at a point \(c \in \mathcal{X}\) if \(f(x) > f(c)\) for every \(x\) in an open interval around \(c\). The minimum value across all local minima is defined as the global minimum. This will be another crucial point of this course as this is a research field on its own. Much of machine learning is tied to the riddle of finding the best solution to a problem - e.g. finding the lowest cost.

Example of a global and local minimum/maximum. Source

Looking at this graph it seems quiet obvious to find the minimum and maximum - but when we working in non-imaginary and viewable dimensions we can not take a look at it. Also in order to take a look at a graph we need to calculate every point of it which can get quite tricky at higher dimensions.

Before taking a look at the problem of higher dimensions we want to define a way no how to calculate the local and global minimum.

Derivative

The derivative \(f'\) of a function \(f\) is a function which describes the growth and decrease of the function \(f\). A function \(f: \mathcal{A} \rightarrow \mathcal{B}\) is derivable at a point \(a \in \mathcal{A}\) if

\[\lim_{x \rightarrow x_0} = \frac{f(x) - f(x_0)}{x-x_0}\]

exists. If we replace \(x\) with \(x_0+h\) we obtain

\[\lim_{h \rightarrow 0} = \frac{f(x_0 + h) - f(x_0)}{h} := f'(x_0)\]

which describes the derivative of \(f\) at the point \(x_0\). Understanding the meaning of this is not trivial but basically it limits the growth of a function within a region.

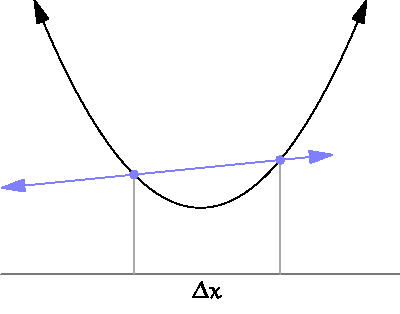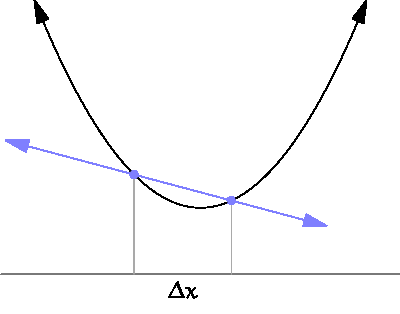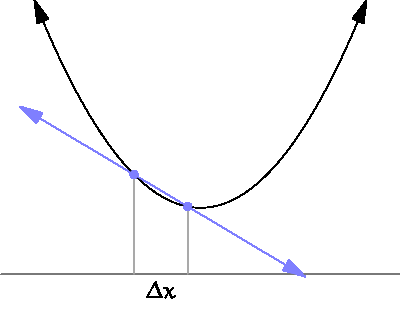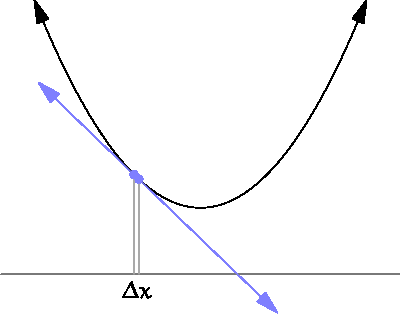
By approaching \(\Delta x \rightarrow 0\) we obtain a tangent which describes the growth at the point \(x\). Source

The derivative of the basic function \(f: \mathbb{R} \rightarrow \mathbb{R}\) for \(f(x)=x^2\) is \(f'(x)=2x\). The second order derivative \(f''\) is defined as the derivative of the derivative - in our example it is \(f''=2\) and \(f''' = f^{(3)} = 0\). The reverse procedure of derivation is called integration of a function.

Not every function is differentable. E.g. \(f: \mathbb{R} \rightarrow \mathbb{R}\) with \(f(x)=|x|\) is not differentable at \(x=0\). This will become important when working with neural networks. Source

Working with vectors and matrices

After we have defined vectors and matrices in Data structures we also want to take a look at how to work with them.

Vector operations

The sum of two vectors \(\text{a},\text{b}\) is defined by

\[\text{a} + \text{b} = [a_1 + b_1, a_2 + b_2, \dots, a_m + b_m]\]

We see that this definition can only be applied if the dimensions of both vectors match. If they do not match the addition of 2 vectors is not defined.

We can scale our vector \(\text{a}\) by multiplying a scalar \(c\) to it which is defined by

\[c\text{a} = [ca_1, ca_2, ..., cx_m]\]

The dot product \(\cdot\) of two vectors \(\text{a}, \text{b}\) is given by

\[\text{a} \cdot \text{b} = \sum_{i=1}^{m} a_i b_i\]

which returns a scalar. Once again this is only defined if both dimensions match.

Matrix operations

The addition of two \(m \times n\) matrices \(\text{A},\text{B}\) is defined as

\[\begin{split}\text{A} + \text{B} = \begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix} + \begin{pmatrix} b_{1,1} & \cdots & b_{1,n} \\ \vdots & \ddots & \vdots \\ b_{m,1} & \cdots & b_{m,n} \end{pmatrix} = \begin{pmatrix} a_{1,1} + b_{1,1} & \cdots & a_{1,n} + b_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} + b_{m,1} & \cdots & a_{m,n} + b_{m,n} \end{pmatrix}\end{split}\]

We see that the resulting matrix is again a \(m \times n\) matrix. The common rules of associativity and commutativity also apply here.

More interesting is the multiplication of the \(m \times n\) matrix \(\text{A}\) with the \(n \times p\) matrix \(\text{B}\) which results in a \(m \times p\) matrix \(\text{C}\) as

\[\begin{split}\text{A} \text{B} = \begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix} \begin{pmatrix} b_{1,1} & \cdots & b_{1,p} \\ \vdots & \ddots & \vdots \\ b_{n,1} & \cdots & b_{n,p} \end{pmatrix} = \begin{pmatrix} c_{1,1} & \cdots & c_{1,p} \\ \vdots & \ddots & \vdots \\ c_{m,1} & \cdots & c_{m,p} \end{pmatrix} = \text{C}\end{split}\]

where \(c_{i,j} = \sum_{k=1}^{n} a_{i,k} b_{k, j}\).

The multiplication of matrices is not commutative as \(\text{A} \text{B}\) returns a \(m \times p\) matrix but \(\text{B} \text{A}\) is not defined if \(m \neq p\).

A visual representation of matrix multiplication. Source

Now lets take a look at the multiplication of a \(m \times n\) matrix \(\text{A}\) with a \(n \times 1\) column vector \(\text{b}\). We say column vector because for this operation we will simply add a single dimension to \(\text{b}\) so it becomes basically a matrix.

\[\begin{split}\text{A} \text{b} &= \begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix} \begin{pmatrix} b_{1} \\ \vdots \\ b_{n} \end{pmatrix} = \begin{pmatrix} a_{1,1}b_1 + \cdots + a_{1,n}b_n \\ \vdots \\ a_{m,1}b_1 + \cdots + a_{m,n}b_n \end{pmatrix}\end{split}\]

The result is a \(m \times 1\) column vector.

When we want to multiply a vector \(\text{v}\) to the left side of a matrix we need to transpose the vector (written as \(\text{v}^\top\) to match the dimensions of the matrix.

\[\begin{split}\text{v} = \begin{pmatrix} v_{1} \\ \vdots \\ v_{n} \end{pmatrix} \Rightarrow \text{v}^\top = \begin{pmatrix} v_{1} & \cdots & v_{n} \end{pmatrix}\end{split}\]

\(\text{v}^\top\) is also called a \(1 \times n\) row vector.

Now our example from above but this time we use a \(m\)-dimensional vector \(d\) instead to match the dimensions:

\[\begin{split}\text{d}^\top \text{A} &= \begin{pmatrix} d_{1} & \cdots & d_{m} \end{pmatrix} \begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix} \\ &= \begin{pmatrix} a_{1,1}d_1 + a_{2,1}d_2 + \cdots + a_{1,m}d_m & \cdots & a_{1,n}d_1 + a_{2,n}d_2 + \cdots + a_{n,m}d_m \end{pmatrix}\end{split}\]

The result is now a \(n\) dimensional row vector.

Statistics

Machine learning is not just statistics on big-data but machine learning relies heavily on statistics to work properly. Statistics helps us to navigate, interpret and understand a dataset and is therefore a mighty tool as it tries to make simplifications on complex structures. A recommended read to dive deeper into the fundamentals of statistics is [FHK+16].

Random variable

A random variable \(X: \Omega \rightarrow \mathbb{R}\) is a function which maps all possible outcomes \(\omega \in \Omega\) of a probability space to \(\mathbb{R}\), so

\[\begin{split}\begin{aligned} X: \Omega &\rightarrow \mathbb{R}\\ \omega &\mapsto X(\omega) = x \end{aligned}\end{split}\]

The realization \(x\) of \(X(\omega) = x\) for \(\omega \in \Omega\) can be regarded as an outcome of an experiment, also called an event. We will define events with

\[\begin{split}\begin{aligned} \{ X = x \} &\text{ with } \{ \omega : X(\omega) = x \}\\ \{ X \leq x \} &\text{ with } \{ \omega: X(\omega) \leq x \}\\ \{ X \in I \} &\text{ with } \{ \omega \in \Omega | X(\omega) \in I \} \end{aligned}\end{split}\]

where \(I\) is an interval on \(\mathbb{R}\).

Example

To understand the definitions a bit better it is maybe good to work through an example. Lets say we throw two dices at once and sum up both of their values. All possilblities of the experiment are the tuples \(\Omega = \{ \omega = (i, j), 1 \leq i, j \leq 6 \}\). We define the sum of both dices as a random variable by \(X(\omega) = x = i+j\). Taking a look at the events we can see

\[\begin{split}\begin{aligned} \{ X = 4 \} &= \left\{ (1,3), (2,2), (3,1) \right\}\\ \{ X \leq 4 \} &= \left\{ (1, 1), (1, 2), (1, 3), (2,1), (2, 2), (3, 1) \right\} \end{aligned}\end{split}\]

Density function and distribution

We can also write down the likeliness of the possibilities of a random variable \(X\), also called the probability density function (PDF) \(f\) via

\[\begin{split}f(x) = \begin{cases} \mathbb{P}_X \left[ X = x_i \right] = p_i, &x = x_i \in \lbrace x_1, x_2, \dots \rbrace \\ 0, &\text{otherwhise} \end{cases}\end{split}\]

This tells us how likely a certain event of our probability space is likely to occur. Most of the time we are interested in this distribution rather than the mapping of the random variable because this is often unknown and is one of the topics of statistics to re-construct this mapping.

We also often work with the cumulative distribution function (CDF), also often just called the distribution function, of a random variable \(X\) defined by

\[F_X (x) = \mathbb{P}_X \left[ X \leq x \right] = \sum_{i:x_i \leq x} f(x_i)\]

Example

Considering a coin drop \(X\) with probability space \(\Omega = \{ 0, 1 \}\) where \(0\) maps to heads and \(0\) to tails we can provide the probability density function via

\[\begin{split}\mathbb{P}_X(x) = \begin{cases} \frac{1}{2}, &x = 0\\ \frac{1}{2}, &x = 1\\ \end{cases}\end{split}\]

as both events are equally likely.

Continuous random variables

When we do not want to limit us to working with discrete random variables we need to refine the definitions when working with continuous random variables. Lets say we have a random variable \(X\) which can be any value between 0 and 1. As there are infinite many rational numbers between 0 and 1 the question remains how we can map a probability to each of these values without making the sum of possibilities of all possible events exceed 1.

Because of this we call a random variable \(X\) continuous if there exists a density function \(f(x) \geq 0\) that for an interval \([a, b]\)

\[\mathbb{P} [a \leq X \leq b] = \int_a^b f(x) dx\]

There are certain requirements to such a density function like \(\int_{- \infty}^\infty f(x) dx = 1\) as the sum of all probabilities can not exceed 1 but also must some up to 1. The circumstance that a single value of a continuous random variable has the likelihood of 0 is now clear because

\[\mathbb{P} [ X = a ] = \mathbb{P} [ a \leq X \leq a ] = \int_a^a f(x) dx = F(a) - F(a) = 0\]

The distribution \(F_X\) of a continuous random variable \(X\) with density function \(f\) is defined by

\[F_X (x) = \mathbb{P} [ X \leq x ] = \int_{- \infty}^{x} f(x) dx\]

Quantiles

\(x_p\) is a p-quantile of a random variable \(X\) if

\[\begin{split}\begin{aligned} \mathbb{P}[X \leq x_p] \geq p \\ \mathbb{P}[x_p \leq X] \geq (1-p)\\ \end{aligned}\end{split}\]

An important p-quantile is for \(p=0.5\) which is commonly referred to as the median and must not be the same as the mean.

A common probability density function is the standard normal distribution. Here it is displayed with its quantiles. Source

Expectation and variance

The expectation \(\mathbb{E}[X]\) of a discrete random variable \(X\) with \(\Omega = \{ x_i \}_{i=1}^{m}\) and density function \(p\) is given by

\[\mu_{X} = \mathbb{E}[X] := \sum_{i=1}^{m} x_i \mathbb{P}(X = x_i) = \sum_{i \geq 1} x_i * p_i\]

For a continuous random variable \(X\) it is with density function \(f_X\) it is defined by

\[\mu_{X} = \mathbb{E}[X] := \int_{- \infty}^{\infty} xf_X(x)dx\]

But most of the time we not solely rely on the expectation of a random variable as a metric but also how far the realizations of the random variable are spread away from the expected value, which is called variance.

The variance \(\sigma^2_X\) of a random variable \(X\) is defined by

\[\sigma^2_X = \text{var}_X = \mathbb{E}[ (X - \mu_X) ]\]

For a discrete random variable \(X\) we can use

\[\sigma^2_X = \text{var}_X = \sqrt{\sum_{\omega \in \Omega} \mathbb{P}(X=\omega) (\omega - \mu_X)^2}\]

and for a continuous random variable \(X\) we use

\[\sigma^2_X = \text{var}_X = \int_{- \infty}^{\infty} (x - \mu)^2 f(x) dx\]

We also often talk about the standard deviation \(\sigma_X\) of a random variable \(X\) which is simply the square root of the variance, so

\[\sigma_X = \sqrt{\text{var}_X}\]

Example

Consider a dice - its possible outcomes are all numbers between 1 and 6, so \(\Omega_{\text{dice}} = \{ 1, 2, 3, 4, 5, 6 \}\). To throw any number is equally likely so \(\mathbb{P}_X(x) = \frac{1}{|\Omega_{\text{dice}}|} = \frac{1}{6}\). Putting everything together we can now calculate the expectation \(\mathbb{E}[X_{\text{dice}}]\):

\[\mu_{X_{\text{dice}}} = \mathbb{E}[X_{\text{dice}}] = \sum_{i=1}^{6} i \frac{1}{6} = 1\frac{1}{6} + 2 \frac{1}{6} + \cdots + 6\frac{1}{6} = 3.5\]

It is important to understand that the expectation itself must not be possible to throw with a dice - it is more like the average value that can be expected.

We create another dice \(\alpha\) - but this time the surface only has only 3 time the number 2 and three times number 5 its 6 sides, so \(\Omega_{\text{dice}_{\alpha}} = \{ 2,5 \}\). We can also calculate the expectation for our new dice:

\[\mu_{X_{\text{dice}_\alpha}} = \mathbb{E}[X_{\text{dice}_\alpha}] = \sum_{i \in \Omega_{\text{dice}_{\alpha}}} i \frac{1}{|\Omega_{\text{dice}_{\alpha}}|} = 2\frac{1}{2} + 5 \frac{1}{2} = 3.5\]

We can use the variance \(\sigma^2\) to still distinguish the random variables from our normal dice and dice \(\alpha\).

\[\begin{split}\begin{aligned} \sigma_{X_{\text{dice}}}^2 &= \frac{\sum_{i=1}^{6} \left(i - \mathbb{E}[X_{\text{dice}}] \right)^2}{6} = \frac{105}{36} \approx 2.916667\\ \sigma_{X_{\text{dice}_\alpha}}^2 &= \frac{\sum_{i \in \{ 2, 5 \}} \left(i - \mathbb{E}[X_{\text{dice}_\alpha}] \right)^2}{2} = \frac{9}{4} = 2.25 \end{aligned}\end{split}\]

Precision and recall

As a big part of machine learning is based on classification we need to learn the most basic terms to understand the rate our estimator.

\[\begin{split}\begin{aligned} \text{precision} &= \frac{\# \{ \text{True positive predictions} \}}{\# \{ \text{Positive predictions} \}}\\ \text{recall} &= \frac{\# \{ \text{True positive predictions} \}}{\# \{ \text{Positive examples} \}}\\ \end{aligned}\end{split}\]

Illustration of precision and recall. Source.

Bibliography Dimensionality in SuperCollider